本文共 1013 字,大约阅读时间需要 3 分钟。
今天Smartbi给大家分享 热销车型分类排名总表 这张移动端报表的制作过程。

制作工具:Smartbi云报表
Smartbi云报表是一款基于Office Excel的SAAS BI工具,支持在Excel端结合云端数据和本地数据进行处理、分析,可以一键生成动态、静态图表,能够将结果发布至移动端,用户可以随时随地查看、分享、点评,实现协同办公。

-
极简的架构,用户不用安装“服务器”;
-
安装插件后用手机、QQ、微信直接登录;
-
Excel一键直达APP实现移动报表。
注:由于定位的区别,云报表插件不能和Smartbi电子表格插件兼容!
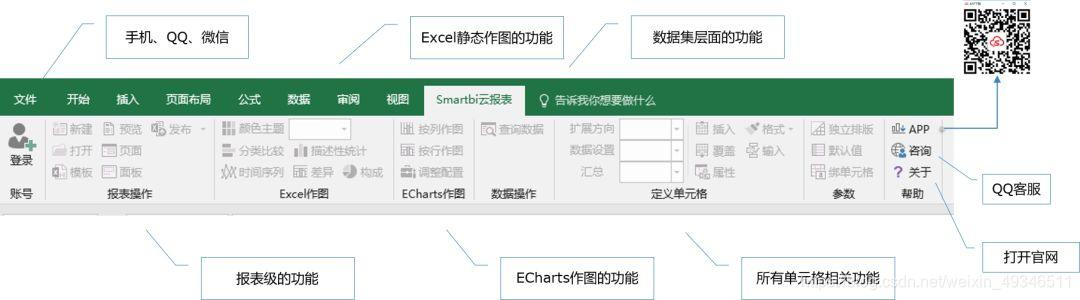
图:Smartbi云报表的Excel插件功能
示例教程
通过云报表的查询条件设置参数,以云端“主流热销乘用车数据”为例,实现查询条件下的数据展示。效果如下:
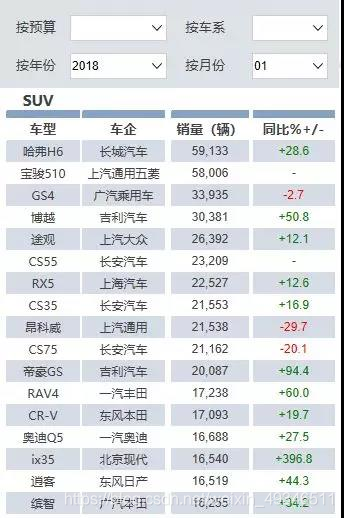
实现步骤
1、查询数据集
在Excel中登录服务,点击查询数据,选择业务查询-主流热销乘用车:
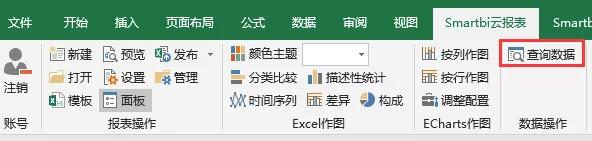
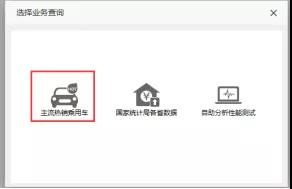
2、拖拽字段设置查询和展示数据
通过拖拽基础表的字段方式来设置查询条件和展示内容,根据需要进行参数修改。
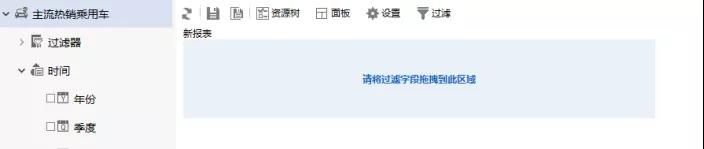
左侧资源树区勾选需要字段:预算、车系、年份、月份、车型、车企、车类、销量,勾选字段会在面板区显示,拖拽查询条件字段至过滤区,展示字段在行区,度量数据在度量区。点击过滤展示区上侧刷新按钮,即可展示数据。
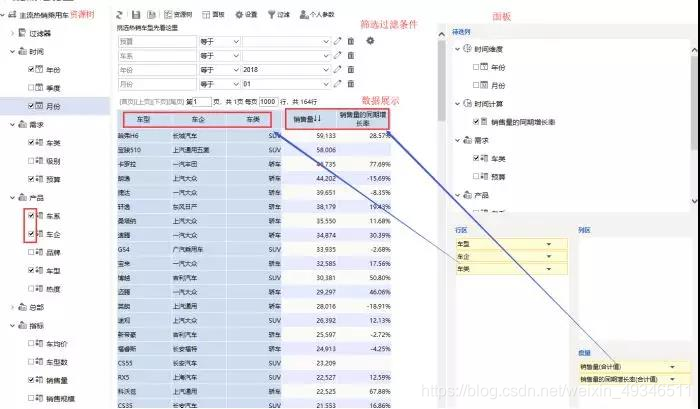
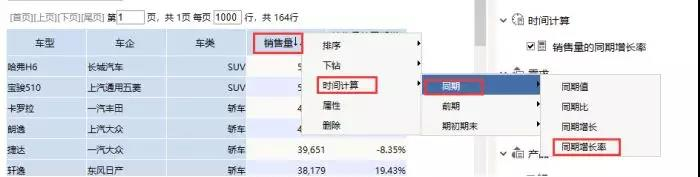
此处要特别说明的是同比增长率设置,如下图:销售量右击-时间计算-同期-同期增长率,还可进行排序等操作。
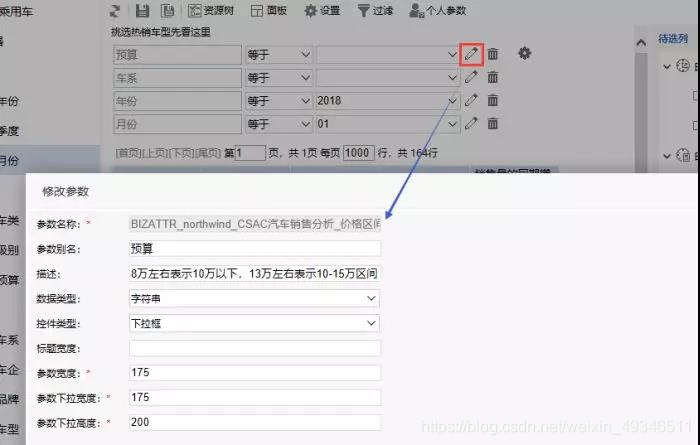
修改参数操作:点击右侧编辑按钮,如此示例中控件类型为下拉框。
字段设置完成后,保存个人参数,可重命名(如个人参数未显示,可进行多次保存重新打开尝试)。
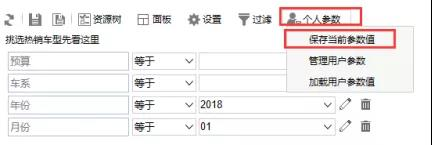
最后点击上侧保存按钮,重命名保存到我的空间。
3、创建电子表格
新建电子表格,并绘制静态表样如下:

4、电子表格与空间数据关联设置
关联展示内容:将数据集面板中对象的字段直接拖拽到相应的单元格中,选择方式为:插入。


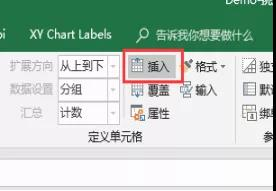
车类SUV和轿车分别展示,单元格还需设置过滤方式:双击单元格-单元格属性-过滤:车类等于SUV或轿车。

关联查询条件:独立排版,将参数拖拽到布局下方:并绑定对应的单元格即可。

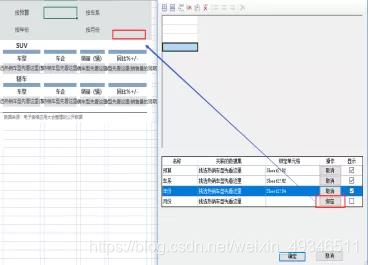
条件格式设置:设置电子表格间隔色公式为"=MOD(ROW(), 2) = 1
正负增长趋势字体颜色自定义:[绿色]0.0%;[红色]-0.0%;-。

5、发布与预览
点击发布-选择保存位置-重命名-保存即可。预览功能为先保存后预览。
请使用与Excel插件端相同的账号登陆APP查看
转载地址:http://rhvaz.baihongyu.com/